Изчислете реакциите на гредата върху две опори. Изчислителна и графична работа. Определяне на опорните реакции на лъча. Процедурата за решаване на проблеми за определяне на реакциите на опорите на гредата

Имайте представа за видовете опори и реакциите, които се случват в опорите.

Да познава трите форми на уравненията на равновесието и да може да ги използва за определяне на реакциите в опорите на системите от греди.

Умейте да проверявате правилността на решението.

Видове товари и видове опори

Видове товари

Според метода на приложение товарите се разделят на

· фокусирани и

· разпределени.

Ако действителното прехвърляне на натоварване се извършва върху пренебрежимо малка площ (в точка), натоварването се нарича концентрирано.

Често натоварването се разпределя върху значителна площ или линия (водно налягане върху язовира, сняг върху покрива и т.н.), тогава натоварването се счита за разпределено.

При проблеми със статиката за абсолютно твърди тела, разпределеното натоварване може да бъде заменено с резултантното натоварванеконцентрирана сила (фиг. 6.1).

р- интензивност на натоварването; I е дължината на пръта;

G = ql- резултатна от разпределения товар.

Видове опори за гредови системи(вижте лекция 1)

Гредата е конструктивна част под формата на права греда, фиксирана върху опори и огъната от сили, приложени към нея.

Височината на сечението на гредата е незначителна спрямо дължината.

Твърдо уплътнение (прищипване)(фиг. 6.2)

Опората не позволява движение или завъртане. Уплътнението се заменя с два силови компонента Ракси и двойка с момента Г-н.

За да се определят тези неизвестни, е удобно да се използва система от уравнения във формата

Всяко уравнение има едно неизвестно количество и се решава без замествания.

За да се контролира правилността на решенията, се използва допълнително уравнение на моментите спрямо всяка точка на гредата, напр.

Артикулираща опора(фиг. 6.3)

Опората позволява въртене около пантата и движение по опорната повърхност. Реакцията е насочена перпендикулярно на опорната повърхност.

Шарнирно-фиксирана опора(фиг. 6.4)

Опората позволява въртене около шарнир и може да бъде заменена от два компонента на силата по координатните оси.

Греда на две шарнирни опори(фиг. 6.5)

Три сили са неизвестни, две от тях са вертикални, следователно е по-удобно да се използва система от уравнения във втората форма за определяне на неизвестните:

Моментните уравнения се съставят спрямо точките на закрепване на гредата. Тъй като моментът на силата, преминаваща през точката на закрепване, е 0, в уравнението ще остане една неизвестна сила.

За контрол на правилността на решението се използва допълнително уравнение

В равновесието на твърдо тяло, където можете да изберете три точки, които не лежат на една и съща права линия, е удобно да използвате система от уравнения в третата форма (фиг. 6.6):

Примери за решаване на проблеми

Пример 1. Едноопорна (притисната) греда е натоварена с концентрирани сили и двойка сили (фиг. 6.7). Определете реакциите на вграждане.

2. Може да възникне реакция във вграждането, представена от два компонента: (Р да,Р брадва), и реактивен въртящ момент M A . Начертаваме възможните посоки на реакции върху диаграмата на лъча.

Коментирайте.Ако посоките са избрани неправилно, по време на изчисленията ще получим отрицателни стойности на реакцията. В този случай реакциите в диаграмата трябва да бъдат насочени в обратна посока, без да се повтаря изчислението.

Поради ниската височина се счита, че всички точки на лъча са на една и съща права линия; и трите неизвестни реакции се прилагат в една точка. За да го решите, е удобно да използвате системата от уравнения на равновесие в първата форма. Всяко уравнение ще съдържа едно неизвестно.

3. Използваме система от уравнения:

Знаците на получените реакции са (+), следователно посоките на реакциите са избрани правилно.

3. За да проверим правилността на решението, създаваме уравнение на моменти около точка B.

Заменяме стойностите на получените реакции:

Решението е попълнено правилно.

Пример 2.Двойна опорна греда с шарнирни опори АИ INнатоварени с концентрирана сила Е,разпределено натоварване с интензивност ри няколко сили с момент T(фиг. 6.8а). Определете реакциите на опорите.

Решение

1. Лява опора (точка а)- подвижна панта, тук реакцията е насочена перпендикулярно на опорната повърхност.

Дясната опора (точка B) е фиксирана панта, тук начертаваме два компонента на реакцията по координатните оси. ос оподравнен с надлъжната ос на гредата.

2. Тъй като в диаграмата ще се появят две неизвестни вертикални реакции, не е препоръчително да се използва първата форма на уравненията на равновесието.

3. Заменете разпределения товар с концентриран:

G = ql; G= 2*6 = 12 kN.

Поставяме концентрираната сила в средата на обхвата, след което проблемът се решава с концентрирани сили (фиг. 6.8, b).

4. Начертаваме възможните реакции в опорите (посоката е произволна).

5. За да решите, изберете уравнението на равновесието във формата

6. Съставяме уравнения на моменти спрямо точките на закрепване:

Следователно реакцията е отрицателна Р И y трябва да бъде насочен към противоположната страна.

7. Използвайки проекционното уравнение, получаваме:

R Bx- хоризонтална реакция в опора B.

Реакцията е отрицателна, следователно в диаграмата нейната посока ще бъде противоположна на избраната.

8. Проверка на верността на решението.За да направим това, използваме четвъртото уравнение на равновесието

Нека заместим получените стойности на реакцията. Ако условието е изпълнено, решението е правилно:

5,1 - 12 + 34,6 – 25 -0,7 = 0.

Пример 3.Определете опорните реакции на гредата, показана на фиг. 1.17, А.

Решение

Помислете за равновесието на гредата AB.Нека отхвърлим опорната фиксация (вграждане) и заменим нейното действие с реакции НА, V A И т А(фиг. 1.17, b). Получихме плоска система от произволно разположени сили.

Избираме координатна система (фиг. 1.17.6) и съставяме уравнения на равновесие:

Нека създадем тестово уравнение

следователно реакциите се определят правилно.

Пример 4.За дадена греда (фиг. 1.18, А) определят реакциите на подкрепа.

Решение

Отчитане на равновесието на лъча AB.Изхвърляме опорните закрепвания и заменяме тяхното действие с реакции (фиг. 1.18.6). Получихме плоска система от произволно разположени сили.

Избираме координатна система (виж фиг. 1.18.6) и съставяме уравнения на равновесие:

q 1,

Разстояние от точката А q 1 (a + b);

Резултат от равномерно разпределения интензитет на натоварване q 2;

Разстояние от точката Акъм линията на действие на резултанта q 2 (d - c).

Замествайки числовите стойности, получаваме

от където V B = 28,8 kN;

- разстояние от точката INкъм линията на действие на резултантното q 1 (a+b);

- разстояние от точката INкъм линията на действие на резултата q 2 (d - c).

където V A= 81,2 kN.

Нека създадем тестово уравнение:

Пример 5.За дадена прътова система (фиг. 1.19, А) определят силите в прътите.

Решение

Помислете за равновесието на гредата AB,към които се прилагат както дадени, така и желани сили.

Лъчът е подложен на равномерно разпределено натоварване от интензитет q,сила Р и концентриран момент T .

Нека освободим лъча от връзките и заменим тяхното действие с реакции (фиг. 1.19, b). Получихме плоска система от произволно разположени сили.

Изберете координатна система (вижте Фиг. 1.19, b) и съставете уравненията на равновесието:

Където q(a + б)- резултатна

равномерно разпределен интензитет на натоварване р(на чертежа е показано с прекъсната линия).

Като заместим числовите стойности, получаваме:

откъдето N AC = 16 kN;

Нека си припомним, че сумата от проекциите на силите, образуващи двойка върху всяка ос, е равна на нула;

Където NBD cos α N BD ", N BF cos β- вертикална компонента на силата нБ Е(линии на действие на хоризонтални компоненти на силите NBDИ N BFпреминават през точка Аи следователно техните моменти относно точката Аса равни на нула). Заместване на числови стойности и отчитане на това нБ д = 1,41N BFполучаваме:

където нБ Е = 33,1 kN.

Тогава N BD = 1,41*33,1 = 46,7 kN.

За определяне на силите в прътите не е използвано уравнението на равновесието: ΣP до = 0.Ако силите в прътите са определени правилно, тогава сумата от проекциите върху оста vна всички сили, действащи върху гредата, трябва да е нула. Проектиране на всички сили върху оста v,получаваме:

следователно силите в прътите са определени правилно.

Пример 6.За дадена плоска рамка (фиг. 1.20, А) определят реакциите на подкрепа

Решение

Освобождаваме рамката от връзките и заменяме тяхното действие с реакции N A, V A, V B (фиг. 1.20, b). Получихме плоска система от произволно разположени сили.

Изберете координатна система (вижте фиг. 1.20, b) и съставете уравненията на равновесието:

Където Р 2 cos α- вертикална компонента на силата P 2;

P 2 sin α- хоризонтална компонента на силата P 2;

2qa- резултат от равномерно разпределен интензитет на натоварване р(показано с пунктирана линия);

откъдето V B = 5,27 qa;

където H A =7qa

силова линия R 2 cos α минава през точка INи следователно неговия момент около точката INравен на нула

където V A = 7qa.

Уравнението на равновесието Σ не е използвано за определяне на реакциите P iv =0.Ако реакциите са определени правилно, тогава сумата от проекциите върху оста vна всички сили, действащи върху рамката, трябва да бъде нула. Проектирайки всички сили върху оста v, получаваме:

следователно опорните реакции се определят правилно.

Нека си припомним, че сумата от проекциите на силите, образуващи двойка с момента T,на която и да е ос е нула.

Тестови въпроси и задачи

1. Заменете разпределеното натоварване с концентрирано и определете разстоянието от точката на прилагане на резултата до опората А(фиг. 6.9).

2. Изчислете стойността на общия момент на силите на системата спрямо точката А(фиг. 6.10).

3. Коя форма на уравнения на равновесие е препоръчително да се използва при определяне на реакциите при вграждане?

4. Каква форма на системата от уравнения на равновесие е препоръчително да се използва при определяне на реакциите в опорите на двуподпорна греда и защо?

6. Определете вертикалната реакция в вграждането за гредата, показана на фиг. 6.11.

ПРИМЕРИ ЗА РЕШАВАНЕ НА ЗАДАЧИ ПО СТАТИКА

Пример 1.Определете реакциите на опорите на хоризонтална греда при дадено натоварване.

дадени:

Диаграма на лъча (фиг. 1).

П= 20 kN, Ж= 10 kN, М= 4 kNm, р= 2 kN/m, а=2 м, b=3 м, .

___________________________________

АИ IN.

Ориз. 1

Решение:

Помислете за равновесието на гредата AB(фиг. 2).

Към гредата се прилага балансирана система от сили, състояща се от активни сили и сили на реакция.

Активен (дадени) сили:

Двойка сили с момент М, Където

Концентрирана сила, заместваща действието, разпределено по протежение на сегмент ACинтензивност на натоварването р.

величина

Линията на действие на силата минава през средата на сегмента AC.

Реакционни сили (неизвестни сили):

Замества действието на изхвърлена подвижна става (опора А).

Реакцията е перпендикулярна на повърхността, върху която лежат ролките на подвижната става.

Заменя действието на изхвърлена фиксирана панта (подпора IN).

Компоненти на реакция, чиято посока е предварително неизвестна.

Изчислителна схема

Ориз. 2

За получената плоска произволна система от сили могат да се съставят три уравнения на равновесие:

Задачата е статично определима, тъй като броят на неизвестните сили (,,) е три - равен на броя на уравненията на равновесието.

Нека поставим координатната система XYточно А, ос БРАВИЛАНека го насочим по гредата. Нека изберем точка като център на моментите на всички сили IN.

Нека създадем уравнения на равновесие:

Решавайки системата от уравнения, намираме ,,.

След като определихме, намираме големината на силата на реакция на фиксираната панта

За да проверим, нека създадем уравнението

Ако в резултат на заместване в дясната страна на това равенство на данните от задачата и намерените сили на реакция получим нула, тогава проблемът е решен - правилно.

Реакциите бяха намерени правилно. Неточността се дължи на закръгляване при изчисляване.

Отговор:

Пример 2.За дадена плоска рамка определете реакциите на опорите.

дадени:

Рамкова диаграма Фиг. 3

П= 20 kN, Ж= 10 kN, М= 4 kNm, р= 2 kN/m, а=2 м, b=3 м, .

______________________________

Определете реакциите на опорите на рамката.

Ориз. 3

Решение:

Помислете за равновесието на твърда рамка И ТЕГЛО(фиг. 4).

Изчислителна схема

Ориз. 4

Системата от сили, приложени към рамката, се състои от активни сили и сили на реакция.

Активни сили:

Няколко сили с момент , , .

, замени действието на разпределен товар ссегменти VDИ DE.

Линията на действие на силата минава на разстояние от точката IN.

Линията на действие на силата минава през средата на отсечката DE.

Реакционни сили:

Заменя твърдото прищипване, което ограничава всяко движение на рамката в чертожната равнина.

Върху рамката се прилага плоска произволна система от сили. За него можем да създадем три равновесни уравнения:

, ,

Задачата е статистически определима, тъй като броят на неизвестните също е три - , , .

Нека съставим уравненията на равновесието, като изберем точка А за център на моментите, тъй като тя се пресича от най-голям брой неизвестни сили.

Решавайки системата от уравнения, намираме , , .

За да проверим получените резултати, нека създадем уравнение на моменти около точка C.

Замествайки всички стойности, получаваме

Реакциите бяха намерени правилно.

Отговор:

Пример 3. За дадена плоска рамка определете реакциите на опорите.

дадени: версия на проектната схема (фиг. 5);

Р 1 = 8 kN; Р 2 = 10 kN; р= 12 kN/m; М= 16 kNm; л= 0,1 m.

Определете реакциите в опорите АИ IN.

Фиг.5

Решение. Заменяме действието на връзките (подпорите) с реакции. Броят, видът (сила или двойка сили с момент), както и посоката на реакциите зависят от вида на опората. В плоската статика за всяка опора поотделно може да се провери в кои посоки на движение забранява тялото дадената опора. Проверете две взаимно перпендикулярни премествания на тялото спрямо референтната точка ( Аили IN) и въртене на тялото в равнината на действие на външни сили спрямо тези точки. Ако изместването е забранено, тогава ще има реакция под формата на сила в тази посока, а ако въртенето е забранено, тогава ще има реакция под формата на двойка сили с момент ( МА или М IN).

Първоначално реакциите могат да бъдат избрани във всяка посока. След определяне на стойността на реакцията знакът "плюс" ще покаже, че посоката в тази посока е правилна, а знакът "минус" ще покаже, че правилната посока на реакцията е противоположна на избраната (например не надолу, но нагоре за сила или стрелка по часовниковата стрелка, а не срещу нея за момента на няколко сили).

Въз основа на горното, реакциите са показани на фиг. 5. В подкрепа Ате са две, тъй като опората забранява хоризонтално и вертикално движение и въртене около точка А- позволява. Момент МИ не възниква, защото тази шарнирна опора не забранява на тялото да се върти около точката А. В точката INедна реакция, тъй като движението само в една посока е забранено (по протежение на безтегловния лост BB¢ ).

След това трябва да изберете координатните оси x и y и да разложите всички сили и реакции, които не са успоредни на осите, на компоненти, успоредни на тях, като използвате правилото на паралелограма. На фиг. 5 силите , , са разложени. В този случай точката на приложение на резултата и неговите компоненти трябва да са еднакви. Самите компоненти не е необходимо да се обозначават, тъй като техните модули лесно се изразяват чрез модула на резултантната и ъгъла с една от осите, които трябва да бъдат посочени или определени от други зададени ъгли и показани на диаграмата. Например за сила Р 2 модулът на хоризонталната компонента е равен на , а вертикалната компонента - .

Сега можете да създадете три уравнения на равновесие и тъй като има и три неизвестни реакции (,,), техните стойности могат лесно да бъдат намерени от тези уравнения. Знакът на стойността на реакцията, както беше обсъдено по-горе, определя правилността на избраните посоки на реакция. За веригата на фиг. 5 уравнения на проекциите на всички сили върху оста хИ ги уравненията на моментите на всички сили спрямо точката Аще бъде написана така:

От първото уравнение намираме стойността Р B, след което го заместваме с неговия знак в проекционните уравнения и намираме стойностите на реакцията хА и UА.

В заключение отбелязваме, че е удобно да съставим уравнението на моментите спрямо точката, така че да има едно неизвестно в него, т.е. така че тази точка да бъде пресечена от две други неизвестни реакции. Удобно е да изберете осите така, че по-голям брой сили да са успоредни на осите, което опростява изготвянето на проекционни уравнения.

Пример 4.За дадена конструкция, състояща се от два счупени пръта, определете реакциите на опорите и налягането в междинната панта СЪС.

дадени:

Схема на проектиране (фиг. 6).

П= 20 kN, Ж= 10 kN, М= 4 kNm, р= 2 kN/m, а=2 м, b=3 м, .

______________________________________

Определете реакциите на опорите в точките АИ INи налягане в междинната става СЪС.

Ориз. 6

Решение:

Нека разгледаме равновесието на цялата структура (фиг. 7).

Приложено към него:

активни сили,, двойка сили с момент М, Където

сили за реакция:

, , , ,

Замества действието на силното щипане;

Замества действието на шарнирно подвижна опора А.

Изчислителна схема

Ориз. 7

За получената плоска произволна система от сили можем да съставим три уравнения на равновесие, като броят на неизвестните е четири, , , .

За да направим задачата статично определима, разделяме конструкцията по вътрешна връзка - панта СЪСи получаваме още две изчислителни схеми (фиг. 8, фиг. 9).

Ориз. 8фиг. 9

Замества действието на тялото ACвърху тялото NE, който се предава през пантата СЪС. Тяло NEпредава ефекта си върху тялото ACпрез същата панта СЪС, Ето защо ; , .

За три проектни схеми можем да създадем общо девет уравнения на равновесие, а броят на неизвестните е шест, , , , , , , т.е. проблемът е станал статично определим. За да решим проблема, използваме Фиг. 8, 9 и фиг. 7 ще бъдат оставени за проверка.

Тяло слънце(фиг. 8)

Тяло SA(фиг. 9)

4)

5)

6)

Решаваме система от шест уравнения с шест неизвестни.

Преглед:

Реакциите на външните опори в точките A и B са намерени правилно. Налягането в съединението C се изчислява по формулата

Отговор: , , , ,

Минусите означават, че посоките трябва да се обърнат.

Пример 5.Дизайнът се състои от две части. Определете кой метод за свързване на части от конструкцията има най-малък модул на реакция и за тази опция за свързване определете реакциите на опорите, както и връзките СЪС.

дадени:= 9 kN; = 12 kN; = 26 kNm; = 4 kN/m.

Диаграмата на проектиране е показана на фиг. 10.

Фиг.10

Решение:

1) Определяне на реакцията на опора А при шарнирно свързване в точка С.

Нека разгледаме система от балансиращи сили, приложени към цялата конструкция (фиг. 11). Нека съставим уравнение за моментите на силите спрямо точката Б.

Фиг.11

където kN.

След заместване на данни и изчисления, уравнение (26) приема формата:

(2)

Получаваме второто уравнение с неизвестни, като разглеждаме системата от балансиращи сили, приложени към частта от конструкцията, разположена вляво от пантата СЪС(фиг. 12):

Ориз. 12

От тук намираме това

kN.

Замествайки намерената стойност в уравнение (2), намираме стойността:

Модул на опорна реакция А при шарнирно свързване в точка СЪСе равно на:

2) Изчислителна схема за свързване на части от конструкцията в точка С с плъзгащо уплътнение, показано на фиг. 13.

Ориз. 13

Силовите системи, показани на фиг. 12 и 13 не се различават един от друг. Следователно уравнение (2) остава валидно. За да получите второто уравнение, разгледайте система от балансиращи сили, приложени към частта от конструкцията, разположена отляво на плъзгащото се уплътнение C (фиг. 14).

Ориз. 14

Нека създадем уравнение на равновесие:

и от уравнение (2) намираме:

Следователно модулът на реакция по време на плъзгащо зацепване в панта C е равен на:

Така че, когато е свързан в точка С с плъзгащо се уплътнение, модулът на реакция на опората А е по-малък, отколкото при шарнирно свързване ().

Нека намерим компонентите на реакцията на опората B и плъзгащата се вграждане.

За лявата част на C

,

Ще намерим компонентите на опорната реакция B и момента в плъзгащото се вграждане от уравненията за равновесие, съставени за частта от конструкцията вдясно от C.

kN

Отговор: Резултатите от изчислението са показани в таблицата.

Пример 6.

Дадено е: вариант на проектната схема (фиг. 15).

Р 1 = 14 kN; Р 2 = 8 kN; р= 10 kn/m; М= 6 kNm; AB= 0,5 m; слънце= 0,4 m; CD= 0,8 m; DE= 0,3 m; Е.Ф.= 0,6 m.

Определете реакциите в опорите АИ Е.

Решение. Използвайки препоръките на пример 3, подреждаме реакциите в опорите. Те са четири (, , , ). Тъй като в статиката на равнината е възможно да се конструират само три уравнения на равновесие за едно тяло, тогава за определяне на реакциите е необходимо структурата да се раздели на отделни твърди тела, така че броят на уравненията и неизвестните да съвпада. В този случай тя може да бъде разделена на две тела ABCдИ DEF. Освен това на мястото на разделяне, т.е дза всяко от двете тела се появяват допълнителни реакции, определени по вид, брой и посока по същия начин, както при точките АИ Е. Освен това, според третия закон на Нютон, те са равни по стойност и противоположни по посока за всяко от телата. Следователно те могат да бъдат обозначени със същите букви (виж фиг. 16).

Ориз. 15

След това, както в пример 3, заместваме разпределеното натоварване рконцентрирана сила и намерете нейния модул. След това избираме координатните оси и очертаваме всички сили на фиг. 15 и 16 на компоненти, успоредни на осите. След това съставяме уравнения на равновесие за всяко от телата. Има общо шест от тях и има също шест неизвестни реакции (, , , , , ), така че системата от уравнения има решение и е възможно да се намерят модулите и като се вземе предвид знакът на модула , правилната посока на тези реакции (вижте пример 3).

Ориз. 16.Разделяне на структура на две тела в една точка д, т.е. в точката на свързването им чрез плъзгащо уплътнение (триенето не се взема предвид)

Препоръчително е да изберете последователността на съставяне на уравненията по такъв начин, че от всяко следващо да е възможно да се определи една от желаните реакции. В нашия случай е удобно да започнем с тялото DEF, защото за него имаме по-малко неизвестни. Първо, нека създадем уравнение за проекции върху оста Х,от които ще намерим РЕ. След това ще съставим уравнения на проекции върху осите прии ще намерим Y D, и след това уравнението на моментите около точката Еи дефинирайте МД. След това преминаваме към тялото ABCD. За него първото нещо, което можете да направите, е да създадете моментни уравнения относно точката Аи намери М A, а след това последователно от уравненията на проекциите върху оста намерете ха, YА. За второто тяло трябва да вземете предвид реакциите си Yд М D, като ги вземем от фиг. 16, но стойностите на тези реакции вече ще бъдат известни от уравненията за първото тяло.

В този случай стойностите на всички предварително определени реакции се заместват в последващи уравнения със собствен знак. Така уравненията ще бъдат написани така:

за тяло DEF

за тяло ABCD

В някои изпълнения, коефициентът на триене е определен в някакъв момент, например. Това означава, че в този момент е необходимо да се вземе предвид силата на триене, където нА е реакцията на самолета в тази точка. Когато конструкцията се раздели в точката, където се отчита силата на триене, всяко от двете тела е обект на собствена сила на триене и реакция на равнината (повърхността). Те са противоположно насочени по двойки и еднакви по стойност (както и реакциите на фиг. 16).

реакция нвинаги перпендикулярна на равнината на възможното плъзгане на телата или допирателна към повърхностите в точката на плъзгане, ако там няма равнина. Силата на триене е насочена по тази допирателна или по равнината срещу скоростта на възможното плъзгане. Горната формула за силата на триене е валидна за случая на гранично равновесие, когато плъзгането е на път да започне (при негранично равновесие силата на триене е по-малка от тази стойност и нейната стойност се определя от уравненията на равновесието). По този начин, във вариантите за определяне на граничното равновесие, като се вземе предвид силата на триене, е необходимо да се добави още едно уравнение към уравненията на равновесието за едно от телата. Когато се вземе предвид съпротивлението при търкаляне и се посочи коефициентът на съпротивление при търкаляне, се добавят уравненията за равновесие на колелото (фиг. 17).

При гранично равновесие

Фиг.17

От последните уравнения, знаейки G , ,R,може да се намери Н,Е tr, Tда започне да се търкаля, без да се подхлъзне.

В заключение отбелязваме, че структурата е разделена на отделни тела на мястото (точката), където се извършва най-малък брой реакции. Често това е безтегловен кабел или безтегловен ненатоварен лост с панти в краищата, които свързват две тела (фиг. 18).

Ориз. 18

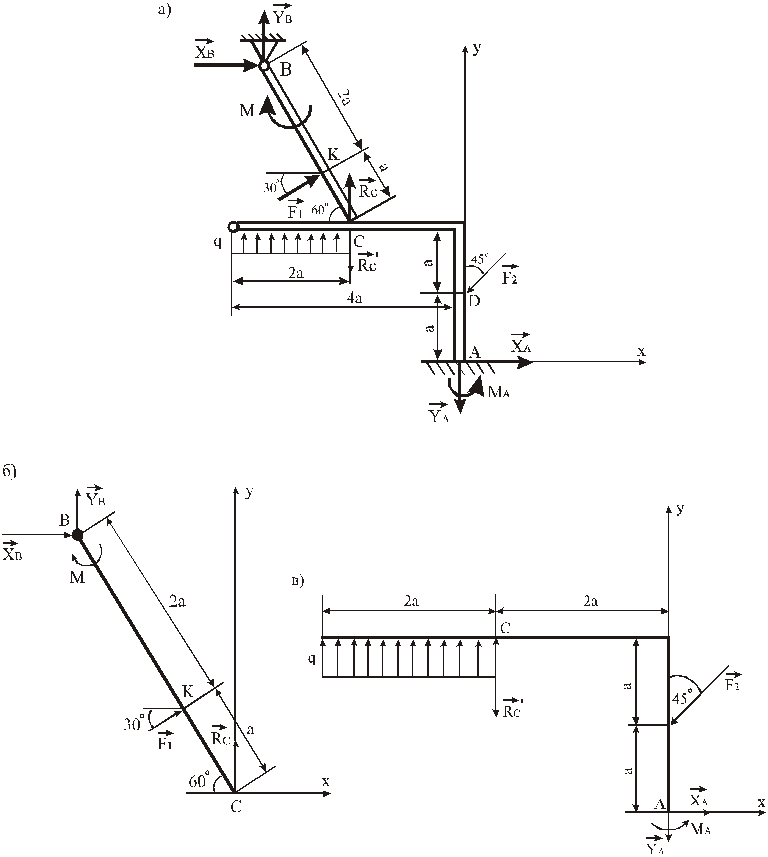
Пример 7. Твърда рамка ABCD(фиг. 19) има в точката Афиксирана шарнирна опора, Ав точката b- подвижна шарнирна опора върху ролки. Всички ефективни натоварвания и размери са показани на фигурата.

дадени: Е=25 kN, =60º, Р=18 kN, =75º, М= 50 kNm, = 30°, а= 0,5 м.

Определете: реакции в точки АИ IN , причинени от действащи натоварвания.

Ориз. 19

Упътвания.Задачата е да се уравновеси тяло под действието на произволна равнинна система от сили. Когато го решавате, вземете предвид, че напреженията на двата клона на нишката, хвърлени върху блока, когато се пренебрегне триенето, ще бъдат еднакви. Моментното уравнение ще бъде по-просто (съдържа по-малко неизвестни), ако уравнението е написано спрямо точката, където линиите на действие на две реакции на връзката се пресичат. При изчисляване на момента на силатаЕ Често е удобно да се раздели на компоненти Е' И Е”, за които рамената се определят лесно и използвайте теоремата на Varignon; Тогава

Решение. 1. Помислете за равновесието на плочата. Нека начертаем координатните оси xyи изобразете силите, действащи върху плочата: сила , няколко сили с момент М,напрежение на кабела (по модул T = R)и реакции на връзки (реакция на фиксирана опора на панта АНие го изобразяваме като два компонента, реакцията на шарнирната опора върху ролките е насочена перпендикулярно на опорната равнина).

2. За получената равнинна система от сили съставяме три уравнения на равновесие. При изчисляване на момента на силата спрямо точка АДа използваме теоремата на Вариньон, т.е. Нека разложим компонентите на silu F΄,F ˝ (, )и вземете предвид, че по теоремата на Varignon: Получаваме:

Чрез заместване на числените стойности на дадените количества в съставените уравнения и решаване на тези уравнения ще определим желаните реакции.

Отговор: X =-8,5kN; Y=-23,3 kN; R= 7,3kN. Признаците показват, че силите X АИ У Аса насочени противоположно на силите, показани на фиг. 19.

Пример 8.Твърдата рамка A BCD (фиг. 20) има фиксирана опора на пантата в точка A, а точка D е прикрепена към безтегловен прът. В точка C към рамката е вързан кабел, хвърлен върху блок и носещ товар в края с тегло P = 20 kN. Върху рамката действат двойка сили с момент M = 75 kNm и две сили F 1 = 10 kN и F 2 = 20 kN, сключващи съответно ъгли = 30 0 и = 60 0 с прътите на рамката. Когато определяте размерите на рамката, вземете а =0,2м . Определете реакциите на връзките в точки A и D, причинени от действието на товара.

дадени: P =20 kN, M =75 kNm, F 1 =10 kN, F 2 =20 kN, =30 0, =60 0, =60 0, а = 0,2 м.

Определете: X A, U A, R D.

Ориз. 20

Упътвания.Задачата е да се уравновеси тяло под действието на произволна равнинна система от сили. При решаването му трябва да се има предвид, че напреженията на двата клона на нишката, хвърлени върху блока, когато се пренебрегне триенето, ще бъдат еднакви. Уравнението на момента ще бъде по-просто (съдържа по-малко неизвестни), ако вземем моментите спрямо точката, където линиите на действие на двете реакции на връзката се пресичат. При изчисляване на момента на силата Често е удобно да се раздели на компоненти И , за които рамената се определят лесно и използвайте теоремата на Varignon; Тогава

Решение.

1. Помислете за равновесието на рамката. Нека начертаем координатните оси x, yи изобразяват силите, действащи върху рамката: сили и , двойка сили с момент M, напрежение на кабела (модул T = P) и реакции на реакция (реакция на фиксирана опора на панта Априсъства под формата на компоненти; опората на пръта предотвратява движението на t. D на рамката в посоката на пръта, следователно реакцията на опората ще действа в същата посока).

2. Нека създадем уравнения на равновесие за рамката. За равновесието на произволна равнинна система от сили е достатъчно сумата от проекциите на всички сили върху всяка от двете координатни оси и алгебричната сума на моментите на всички сили спрямо всяка точка от равнината да са равни на нула.

При изчисляване на моменти на сили и спрямо точка АДа използваме теоремата на Вариньон, т.е. нека разложим силите на компоненти, ; , и вземете предвид, че.

Получаваме:

Чрез заместване на числените стойности на дадените количества в съставените уравнения и решаване на тези уравнения ще определим желаните реакции.

От уравнение (3) определяме R D =172,68 kN.

От уравнение (1) определяме X A = -195,52 kN.

От уравнение (2) определяме Y A = -81,34 kN.

Знаците "-" за стойностите X A и Y A означават, че истинската посока на тези реакции е противоположна на тази, посочена на фигурата.

Нека го проверим.

защото тогава реакциите на опорите се намират правилно.

Отговор: X A = -195,52 kN, Y A = -81,34 kN, R D = 172,68 kN.

Пример 9.Конструкцията (фиг. 21) се състои от твърд ъгъл и прът, които в точка С свободно опират един в друг. Външните връзки, наложени на конструкцията са: в точка А - твърда заграда, в точка Б - шарнир. Върху конструкцията действат: двойка сили с момент M = 80 kN m, равномерно разпределен интензитет на натоварване р=10 kN/m и сили: =15 kN и =25 kN. Когато определяте размерите на конструкцията, вземете А=0,35 m. Определете реакциите на връзките в точки A, B и C.

дадени: M = 80 kN · m, р=10 kN/m, F 1 =15 kN, F 2 =25 kN, А=0,35 m.

Определете: R A, M A, R B, R C.

Упътвания.Задачата е да се уравновеси система от тела под въздействието на равнинна система от сили. Когато го решавате, можете или да разгледате първо равновесието на цялата система, а след това равновесието на едно от телата на системата, изобразявайки го отделно, или веднага да разчлените системата и да разгледате равновесието на всяко от телата поотделно, като вземете съобразете закона за равенство на действията и ответните действия. При задачи, при които има твърдо уплътнение, трябва да се има предвид, че неговата реакция е представена от сила, чийто модул и посока са неизвестни, и двойка сили, чийто момент също е неизвестен.

Решение.

V Извършваме го в съответствие с методологията, описана по-горе.

1. В тази задача изучаваме равновесието на система, състояща се от твърд ъгъл и прът.

2. Изберете координатната система XAU (вижте Фиг. 21).

3. Активните натоварвания на тази система са: разпределено натоварване с интензитет р, , и момент М.

Фиг.21

Нека изобразим на чертежа очакваните реакции на връзките. Тъй като твърдото уплътнение (в напречно сечение А) предотвратява движението на тази част от пръта по посоките хИ U, както и въртене на пръта около точката А, тогава в този участък в резултат на действието на вграждането върху пръта възникват реакции, , . Шарнирна опора в точка INпредотвратява движението на дадена точка на пръта по направленията хИ U. Следователно, в точката INвъзникват реакции и. В точка С на опората на пръта върху квадрата възниква реакцията на действието на квадрата върху пръта и реакцията на действието на пръта върху квадрата. Тези реакции са насочени перпендикулярно на равнината на ъгъла и R C = R ¢ C (според закона за равенство на действието и реакцията).

1. Решаваме проблема с помощта на метода на дисекция. Нека първо разгледаме равновесието на пръта слънце(фиг. 21, b). Върху пръта действат реакциите на връзките, , , сила и момент. За получената равнинна система от сили могат да се съставят три уравнения на равновесие и е по-удобно да се изчисли сумата от моментите на външните сили и реакциите на свързване спрямо точка B:

;;(1)

;; (2)

От уравнение (3) получаваме: R ° С =132,38 kN.

От уравнение (1) получаваме: X B = -12,99 kN.

От уравнение (2) получаваме: У В = -139,88 kN.

Реакция на шарнира в точка B:

Сега разгледайте равновесието на квадрат CA (фиг. 21, V). Върху квадрата действат: реакции на връзка, сила р. Обърнете внимание, че R/C = R C =132,38 kN. За дадена равнинна система от сили могат да се съставят три уравнения на равновесие и сумата от моментите на силите ще се изчисли спрямо точка С:

;;(4)

От уравнение (4) получаваме: X A = 17,75 kN.

От уравнение (5) получаваме: Y A = -143,13 kN.

От уравнение (6) получаваме: M A = -91,53 kNm.

Проблемът е решен.

И сега, за да докажем ясно важността на правилния избор на точка, спрямо която е съставено моментното уравнение, нека намерим сумата от моментите на всички сили спрямо точка А (фиг. 21, V):

От това уравнение е лесно да се определи MA:

MA = -91,53 kNm.

Разбира се, уравнение (6) дава същата стойност на MA като уравнение (7), но уравнение (7) е по-кратко и не включва неизвестните реакции X A и Y A, следователно е по-удобно за използване.

Отговор: R A =144,22 kN, M A = -91,53 kNm, R B =140,48 kN, R C =R ¢ C =132,38 kN.

Пример 10. На площада ABC(), край Акойто е здраво запечатан в точката СЪСлежи на пръта DE(фиг. 22, А). Пръчката има точкадфиксирана шарнирна опора и към нея се прилага сила, а към квадрата - равномерно разпределени по площтари двойка с момент М.

Ориз. 22

Д ано:Е=10 kN, М=5 kNm, q = 20 kN/m, А=0,2 m.

Определете:реакции в точки А , СЪС, дпричинени от дадени натоварвания.

Упътвания.Задачата е да се уравновеси система от тела под действието на равнинна система от сили. Когато го решавате, можете или първо да разгледате равновесието на цялата система като цяло, а след това равновесието на едно от телата на системата, изобразявайки го отделно, или веднага да разделите системата и да разгледате равновесието на всяко от телата отделно, като се вземе предвид закона за равенство на действието и реакцията. В задачи, където има твърда връзка, вземете под внимание, че нейната реакция е представена от сила, чийто размер и посока са неизвестни, и двойка сили, чийто момент също е неизвестен.

Решение. 1. За да определим реакциите, нека анализираме системата и първо да разгледаме равновесието на пръта DE(фиг. 22, b). Нека начертаем координатните оси XYи изобразяват силите, действащи върху пръта: сила , реакция, насочена перпендикулярно на пръта и компонентите и реакциите на шарнира д. За получената равнинна система от сили съставяме три уравнения на равновесие:

,;( 1)

Свободната греда, разгледана в § 2.7, беше натоварена с дадени товари (сили и моменти), които бяха в равновесие (виж Фиг. 3.7). Обикновено определени товари не са взаимно балансирани; неподвижността на конструкцията под въздействието на тези натоварвания се осигурява от наличието на опори, свързващи я с основата. В опорите възникват реакции, които заедно с дадените натоварвания представляват балансирана система от външни сили, действащи върху конструкцията.

Както е известно от курса на теоретичната механика, всяко тяло има три степени на свобода в равнина. Следователно, за да се осигури геометричната неизменност на системата (лъча), е необходимо да се наложат три връзки върху нея (в равнината).

Нека разгледаме различни видове опори за плоски системи.

1. Прищипване или вграждане (фиг. 4.7, а). Прищипаният (или вграден) край на гредата не може нито да се движи напред, нито да се върти. Следователно броят на степените на свобода на греда със захванат край е нула. В опората може да възникне: вертикална реакция (сила R - фиг. 4.7, а), предотвратяваща вертикалното изместване на края на гредата; хоризонтална реакция (сила H), изключваща възможността за нейното хоризонтално изместване и реактивен въртящ момент, предотвратяващ въртенето. По този начин, закрепването на гредата с помощта на вграждане налага три връзки върху нея и осигурява нейната неподвижност.

2. Шарнирна фиксирана опора (фиг. 4.7, b). Напречното сечение на гредата, преминаваща през шарнирно фиксираната опора, не може да се измества транслационно. В опората възниква реактивна сила, преминаваща през центъра на пантата. Неговите компоненти са вертикалната сила R, която предотвратява вертикалното изместване, и хоризонталната сила H, която предотвратява хоризонталното изместване на неподвижното сечение на гредата. Опората не пречи на гредата да се върти спрямо центъра на шарнира и следователно греда, закрепена с една такава опора, има една степен на свобода. Закрепването на гредата с шарнирно фиксирана опора налага две връзки върху нея.

3. Артикулирана подвижна опора (фиг. 4.7, c). Напречното сечение на гредата, преминаваща през шарнирно подвижната опора, може да се движи успоредно на опорната равнина и да се върти, но не може да се движи перпендикулярно на опорната равнина. В опората възниква само една реакция под формата на сила R, перпендикулярна на опорната равнина. Закрепването на гредата с такава опора налага една връзка върху нея.

Разглежданите видове опори също обикновено се изобразяват с помощта на пръти.

Шарнирна подвижна опора е изобразена под формата на прът с панти в краищата (фиг. 5.7, а). Долната панта е неподвижна, а горната може да се движи само по права линия, перпендикулярна на оста на пръта.

Това съответства на условията на закрепване, осигурени от шарнирната подвижна опора (виж фиг. 4.7, c). Опорната реакция действа само по протежение на оста на пръта. Неговите собствени деформации не се вземат предвид при изчисленията, т.е. прътът се счита за безкрайно твърд.

Шарнирна фиксирана опора е изобразена с помощта на два пръта с панти в краищата (фиг. 5.7, b). Горната панта е обща за двете пръчки. Посоките на прътите могат да бъдат произволни. Те обаче не трябва да са разположени на една и съща права линия.

Уплътнението (прищипването) може да бъде представено с помощта на три пръта с панти в краищата, както е показано на фиг. 5.7, c.

Броят на прътите в схематичното представяне на опора е равен на броя на компонентите на опорната реакция и броя на връзките, наложени от тази опора върху конструкцията.

За да не се движи гредата под натоварване, тя трябва да бъде геометрично неизменно (неподвижно) свързана с основата, което при равнинно действие на силите, както вече беше отбелязано, се постига чрез налагането на три външни връзки върху нея.

Това може да стане с помощта на едно вграждане (фиг. 6.7, а) или една шарнирно фиксирана и една шарнирно подвижна опора (фиг. 6.7, б), или с помощта на три шарнирно подвижни опори, чиито посоки на реакция не се пресичат в една точка ( Фиг. 6.7, c).

Ако посоките на три опорни пръта се пресичат в една точка O (фиг. 7.7, a, b), тогава системата е незабавно променлива, тъй като в този случай нито един опорен прът не предотвратява много малко завъртане на гредата около точка O; Това разположение на опорните пръти е неприемливо.

Нека разгледаме геометрично непроменливи системи, състоящи се от няколко греди.

На фиг. 8.7 и, например, показва система от две греди (AB и BC), всяка от които има три връзки. Върху гредата BC се налага една връзка от опорния прът CD, който предотвратява вертикалното изместване на точка C на гредата, и две връзки - шарнир B, който предотвратява вертикалното и хоризонталното изместване на точка B на гредата.

И трите връзки са наложени върху лъч AB чрез вграждане A; шарнир B не може да пречи нито на транслационните премествания, нито на въртенията на лъча AB и следователно не налага никакви връзки върху него.

На фиг. 8.7, b показва геометрично непроменена система, състояща се от три греди (AC, CD и DF). Всеки от тях има три връзки. Така например шарнир C налага две връзки върху лъча CD (тъй като предотвратява хоризонтално и вертикално изместване на точка C), а пантата налага една връзка (тъй като предотвратява само вертикално изместване на точка).

Системите, показани на фиг. 8.7 се наричат ​​шарнирни греди с много участъци.

Общият брой неизвестни опорни реакции за опциите за закрепване на гредата, показани на фиг. 6.7, a, b, c, е равно на три. Следователно, тези реакции могат да бъдат намерени с помощта на три уравнения на равновесие, които са съставени за плоска система от сили. Въз основа на стойностите на опорните реакции и външните натоварвания е възможно да се определят [използвайки формули (2.7) - (4.7)] вътрешните сили във всяко напречно сечение на гредата. Следователно греда, фиксирана чрез налагане на три връзки върху нея, е не само геометрично непроменлива, но и статично определима. Налагането на по-голям брой връзки върху него прави гредата статично неопределена, тъй като в този случай всички опорни реакции не могат да бъдат определени само от уравненията на равновесието.

Уравненията на равновесието, съставени за определяне на опорните реакции, могат да бъдат представени в три различни версии:

1) под формата на суми от проекции на сили върху две произволни оси, които не са успоредни една на друга, и суми от моменти на сили спрямо всяка точка от равнината на MO);

2) под формата на сума от проекции на сили върху произволна ос и две суми от моменти спрямо всякакви точки от равнината, които не лежат на същия перпендикуляр на определената ос на проекциите

3) под формата на три суми от моменти относно всякакви точки от равнината, които не лежат на една и съща права линия

Изборът на един или друг вариант за съставяне на уравненията на равновесието, както и изборът на точките и посоките на осите, използвани при съставянето на тези уравнения, се извършва във всеки конкретен случай по такъв начин, че по възможност съвместното решение на уравнения не се изпълняват. За да проверите правилността на определяне на опорните реакции, се препоръчва да замените получените им стойности във всяко уравнение на равновесие, което не е използвано преди това.

На шарнирна греда с много участъци, показана на фиг. 8.7, а, се прилагат четири външни връзки (три в раздел А и един в раздел С), а върху гредата, показана на фиг. 8.7, b, - пет външни връзки (две в раздел A и по един в раздели B, E и F).

Въпреки това, ако три връзки са наложени на всяка греда, която съставлява шарнирна греда с няколко обхвата, тогава тази греда е статично определена и опорните реакции могат да бъдат намерени от статичните уравнения.

В допълнение към трите уравнения на равновесие за всички сили, действащи върху шарнирна греда с много участъци, са съставени уравнения, които изразяват равенството до нула на моментите на силите, приложени от едната страна на всяка панта (свързваща отделните части на гредата) спрямо центъра на тази панта. Например за гредата, показана на фиг. 8.7, и в допълнение към трите уравнения на равновесие за всички сили, действащи върху него, е съставено уравнение за моментите на левите (или десните) сили спрямо шарнира и за гредата, показана на фиг. 8.7, b, - спрямо панти C и D.

Нека разгледаме пример за определяне на опорните реакции на обикновена греда с един участък, чиято проектна диаграма е показана на фиг. 9.7, а. Да изхвърлим опорите и да заменим влиянието им върху гредата с опорните реакции RA, H и RB (фиг. 9.7, b). Обикновено греда с изхвърлени опори не се изобразява отделно, а обозначенията и посоките на опорните реакции са посочени на проектната диаграма на гредата. Реакциите представляват вертикалните и хоризонталните компоненти на общата реакция на шарнирно фиксираната опора А; силата е пълната реакция на опората B. Посоките на опорните реакции се избират произволно; Ако в резултат на изчислението стойността на всяка реакция се окаже отрицателна, тогава в действителност нейната посока е противоположна на приетата по-рано.

По същия начин съставяме сумата от моментите на всички сили спрямо точка А:

За да проверим намерените стойности на опорните реакции, нека съставим сумата от проекциите на всички сили върху оста y.

Построеното уравнение е изпълнено, което показва правилността на определяне на опорните реакции.

греди ще наричаме прави пръти, които се огъват. По отношение на якостта на материалите терминът „греда“ е много по-широк, отколкото в обичайната употреба на тази дума: от гледна точка на изчисляване на якостта, твърдостта и стабилността, гредата е не само строителна греда, но и вал, болт, ос на вагон, зъб на зъбно колело и др. d.

Първо, ще се ограничим до конструирането на диаграми за най-простия случай на огъване на греда, при който всички дадени товари лежат в една равнина, т.нар. мощност(на фиг. 4, А- равнина P), и тази равнина съвпада с една от основните равнини на лъча. Ще наречем такъв случай плосък завой.

В проектната диаграма е обичайно гредата да се заменя с нейната ос (фиг. 4, b). В този случай всички товари, естествено, трябва

Фигура 4 ще бъде доведена до оста на гредата и равнината на силата ще съвпадне с равнината на чертежа.

По правило гредите имат опорни устройства - опори. За изчисления те са схематизирани под формата на три основни типа опори:

а) шарнирна опора(Фиг. 5, а), в която може да възникне само един компонент на реакцията - , насочен по протежение на опорния прът;

б) шарнирно фиксирана опора(фиг. 5, б), при което могат да възникнат два компонента - вертикална реакция
И хоризонтална реакция

V) щипане(в противен случай силно прищипване или вграждане),където може да има три компонента – вертикален
и хоризонтално
реакции и момент на подкрепа мамо(фиг. 5, V).

Всички реакции и моменти се считат за приложени в точката А- център на тежестта на опорната секция.

Лъчът, показан на фиг. 6, s, наречено просто , или еднопролетен , или двойна опора , и разстоянието лмежду опорите - прелитане .

Конзола наречена греда, която е притисната в единия край и няма други опори (фиг. 4, б), или част от гредата, която виси над опорите (част слънцена фиг. 6, b; части ACИ BD на фиг. 6, е). Банките с висящи части се наричат ​​​​конзолни (фиг. 6, b, V).

За плоска система от сили могат да се съставят три статични уравнения за определяне на неизвестните реакции.

Следователно лъчът ще бъде статично детерминиран, ако броят на неизвестните опорни реакции не надвишава три; в противен случай лъчът е статически неопределен. Очевидно е, че гредите, показани на фиг. 4 и 6 са статично определими.

Лъчът, показан на фиг. 7, А, Наречен непрекъснатои е статично неопределен,тъй като има пет неизвестни реакции на подкрепа: три в подкрепа Аи по един в опорите Б и С.

Чрез поставяне на панти в секциите на гредата, например на точки д И д(Фиг. 7, b), получаваме статично дефинируема шарнирна греда, тъй като всяка такава междинна панта добавя едно допълнително уравнение към трите основни уравнения на статиката: сумата от моменти спрямо центъра на шарнира от всички сили, разположени от едната му страна, е равна на нула .

Конструирането на диаграми за статично неопределени греди изисква възможност за изчисляване на деформации и затова засега ще се ограничим изключително до статично детерминирани греди.

Методите за определяне на опорните реакции се изучават в курса на теоретичната механика. Затова тук ще се спрем само на някои практически въпроси. За да направите това, помислете за обикновен лъч (фиг. 6, а).

1. Подпорите обикновено се обозначават с букви АИ IN.Три неизвестни реакции се намират от следните равновесни уравнения:

а) сумата от проекциите на всички сили върху оста на гредата е равна на нула:
откъде го намират?

б) сумата от моментите на всички сили спрямо опорната панта Аравно на нула:
откъде го намират?
.

в) сумата от моментите на всички сили спрямо опорния шарнир INравно на нула:

откъде го намират?
.

2. За контрол можете да използвате условието, че сумата от проекциите върху вертикалата е равна на нула:

или условието сумата от моменти да бъде равна на нула спрямо някаква точка C, различна от АИ IN,т.е.

U

Състояние
Той е по-лесен за използване, но осигурява надеждна проверка само в случаите, когато върху гредата не се прилагат концентрирани моменти.

3. Преди да съставите уравнения на равновесие, трябва да изберете (най-общо казано произволно) посоките на реакциите и да ги изобразите на фигурата. Ако в резултат на изчисленията някоя реакция се окаже отрицателна, трябва да промените нейната посока във фигурата на обратното и в бъдеще да считате тази реакция за положителна,

5. Ако върху греда действа разпределено натоварване, тогава за определяне на реакциите се заменя с резултатно натоварване, което е равно на площта на диаграмата на натоварването и се прилага в центъра на тежестта на тази диаграма.

Пример 5. Изчислете опорните реакции за гредата, показана на фиг. 8.

Първо, намираме резултатите Р 1 И Р 2 товари, разпределени по площи ACн SV:

;
.

Сила Р 1 се прилага в центъра на тежестта на правоъгълника и Р 2 - в центъра на тежестта на триъгълника. Откриваме реакции:

3.3. Определяне на опорните реакции.

Нека да разгледаме няколко примера.

Пример 3.1.Определете опорните реакции на конзолната греда (фиг. 3.3).

Решение. Представяме реакцията на вграждане под формата на две сили Az и Ay, насочени както е показано на чертежа, и реактивен въртящ момент MA.

Съставяме уравнението на равновесието за гредата.

1. Нека приравним към нула сумата от проекциите върху оста z на всички сили, действащи върху гредата. Получаваме Az = 0. При липса на хоризонтален товар хоризонталната компонента на реакцията е нула.

2. Същото по оста y: сборът на силите е нула. Заменяме равномерно разпределения товар q с резултантния товар qaz, приложен в средата на сечението az:

Ay - F1 - qaz = 0,

Където

Ay = F1 + qaz.

Вертикалната компонента на реакцията в конзолна греда е равна на сумата от силите, приложени към гредата.

3. Съставяме третото уравнение на равновесието. Нека приравним към нула сумата от моментите на всички сили спрямо някаква точка, например спрямо точка А:

Където

Знакът минус показва, че първоначално приетата посока на реактивния момент трябва да бъде обърната. И така, реактивният момент в вграждането е равен на сумата от моментите на външните сили спрямо вграждането.

Пример 3.2.Определете опорните реакции на двуподпорна греда (фиг. 3.4). Такива греди обикновено се наричат ​​прости.

Решение. Тъй като няма хоризонтално натоварване, тогава Az = 0

Вместо второто уравнение може да се използва условието, че сумата от силите по оста Y е равна на нула, което в този случай трябва да се приложи за проверка на решението:
25 - 40 - 40 + 55 = 0, т.е. идентичност.

Пример 3.3.Определете реакциите на опорите на счупена греда (фиг. 3.5).

Решение.

тези. реакцията Ay е насочена не нагоре, а надолу. За да проверите правилността на решението, можете да използвате например условието, че сумата от моментите около точка B е равна на нула.

Полезни ресурси по темата "Определяне на реакциите на подкрепа"

1. който ще даде писмено решениевсяка греда. .
В допълнение към конструирането на диаграми, тази програма също така избира профил на сечение въз основа на условието за якост на огъване и изчислява деформациите и ъглите на завъртане в гредата.

2., който изгражда 4 вида диаграми и изчислява реакции за всякакви греди (дори за статично неопределени).